Расчет треугольника
| СКАЧАТЬ ПРОГРАММУ | Размер |
|---|---|
| Triangle.exe (13570) | 1.03 Мб |
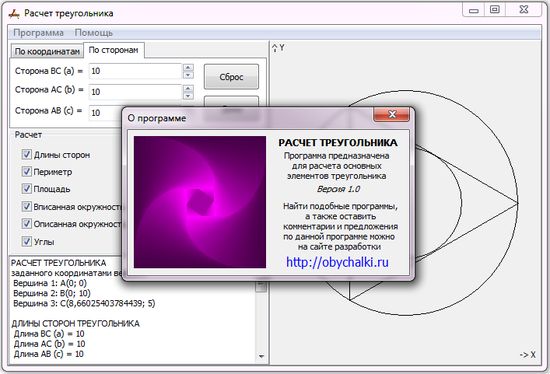
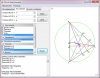
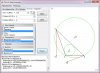
Обучающая программа "Расчет треугольника" позволяет найти площадь, периметр, углы, медианы, высоты и центр тяжести треугольника. Рассчитать параметры вписанной и описанной окружности. Треугольник задается координатами своих вершин или длинами своих сторон или двумя сторонами и углом между ними.
Может использоваться для решения геометрических задач при выполнении школьных и студенческих домашних заданий, служить демонстрационным материалом на уроках геометрии, а также исполнять роль калькулятора при выполнении простых геометрических расчетов.
Для расчетов используются следующие формулы:
Треугольник можно однозначно (с точностью до сдвига и поворота) определить по следующим тройкам основных элементов:
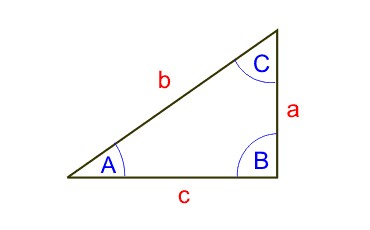
a, b, c — по трем сторонам;
a, b, C — по двум сторонам и углу между ними;
a, B, C — по стороне и двум прилежащим к ней углам.
Сумма углов любого треугольника постоянна
A + B + C = 180°
1. Прямоугольный треугольник. Определение тригонометрических функций.
Угол B = 90° (прямой).
Функция синус: sin(A) = a/b.
Функция косинус: cos(A) = c/b.
Функция тангенс: tg(A) = a/c.
Функция котангенс: ctg(A) = c/a.
2. Прямоугольный треугольник. Тригонометрические формулы.
a = b * sin(A)
c = b * cos(A)
a = c * tg(A)
3. Прямоугольный треугольник. Теорема Пифагора.
b2 = a2 + c2
С помощью теоремы Пифагора можно построить прямой угол, если под рукой нет подходящих инструментов, например, угольника. С помощью двух линеек или двух кусков веревки отмеряем катеты длиной 3 и 4. Потом сдвигаем или раздвигаем их, пока длина гипотенузы не станет равной 5 (32 + 42 = 52).
4. Теорема синусов
a/sin(A) = b/sin(B) = c/sin(C) = 2*R
5. Теорема косинусов
Cos(A) = (b2+c2-a2)/(2*b*c)
6. Формула расчета площади треугольника
S = b*c*sin(A)/2
7. Формула расчета площади треугольника. Формула Герона
S = (p * (p-a) * (p-b) * (p-c))1/2
8. Формула расчета площади треугольника
S = p * (p-a) * tg (A/2)
9. Формула расчета радиуса описанной окружности
R = a/(2*sin(A))
10. Формула расчета радиуса описанной окружности
R= a*b*c /(4*S )
11. Формула расчета радиуса вписанной окружности
R = S/p
12. Формула расчета радиуса вписанной окружности
R = (p-a)*tg(A/2)
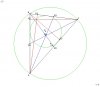
13. Формула расчета центра вписанной окружности
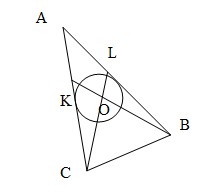
Введем обозначения:
a, b с – стороны BC, AC и AB треугольника,
О – центр вписанной окружности.
xa, xb и xc – абсциссы точек A, B,C соответственно.
ya, yb и yc – их ординаты.
(cx,cy) – координаты точки L.
(bx,by) – координаты точки K.
(x,y) - координаты точки O.
Тогда
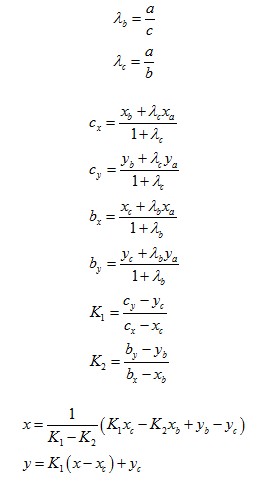
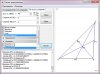
14. Формула расчета центра, описанной около треугольника окружности
ma, mb - коэффициенты наклона линии, проходящих через точки
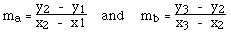
Центр круга - находится на пересечении двух перпендикулярных прямых, проходящих через середины отрезков, образованных вершинами треугольника. Легко доказать, что прямая, перпендикулярная к линии с коэффициентом наклона m имеет коэффициент наклона -1/m, значит уравнения прямых, перпендикулярных a и b и проходящих через середины отрезков будут
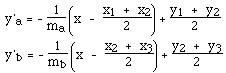
Они пересекаются в центре, и решение относительно x дает
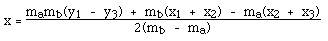
Значение у вычислим подстановкой x в уравнение одного из перпендикуляров.
Примечание:
В программе использован класс TTriangle, реализующий все представленные формулы программным кодом на Delphi (см. страницу "Как рассчитать все параметры треугольника?")
В окне "О программе" используется фрактал "Вложенные квадраты", описанный на странице "Компьютерная графика, фракталы".
150094 просмотра
- Расчет треугольника (13570)
- Калькулятор логических функций (13392)
- Обучающая программа по алгебре "Glance" (5559)
- Таблица умножения в мультфильмах (5441)
- Обучающая программа по арифметике Sapling (3427)
- Тела вращения (Rotation bodies) (2663)
- Магический квадрат (2113)
- Таблица деления в мультфильмах (2042)
- Тестирующая программа по физике PhysicsTest (1786)
- Тестирующая программа по информатике HardTest (1705)
- Тестирующая программа по зоологии AnimalsTest (1653)
- Тестирующая программа по информатике InfTest (1497)
- Тестирующая программа по киноискусству StarsFilmsTest (535)
- Тестирующая программа по звездам эстрады StarsMusicTest (511)
- Тестирующая программа по информатике InfTest (1)
-
vitality ed pills cure for ed or natural ed medications treatment for erectile dysfunction or how to get amoxicillin can i buy amoxicillin over the counter or prednisone 20 mg tablets coupon prednisone 5mg coupon or vacuum pump for ed ed pills for sale
-
erectile dysfunction medication comparison of ed drugs ed cures that work otc ed pills https://canadianpharmacyvikky.com real viagra without a doctor prescription usa ed aids buy prescription drugs online without herbal remedies for ed
-
ed medications over the counter canadian pharmacy vikky best ed drugs new erectile dysfunction treatment https://canadianpharmacyvikky.com ed pills online
Medicament information for patients. What side effects? can i order generic prozac for sale Best information about medicament. Read now.
Наглая воровка Батеенко Наталия Николаевна украла у меня в квартире деньги в сумме один миллион двести тысяч рублей которые я копила на дорогостоящую операцию своему ребенку. Это же надо быть таким подлым человеком как Батеенко Наталья Николаевна чтобы украсть деньги у ребенка от которых зависит его жизнь и здоровье. Я не просто так ее обвиняю, а потому что она только одна имела ключи от квартиры когда занималась уборкой. Несколько месяцев она входила в доверие. Очень качественно и быстро убирала, везде вытирала пыль, даже в труднодоступных местах. Но мне доставляло дискомфорт от того, что посторонний человек находится в квартире и я не могу расслабиться, даже элементарно поговорить по телефону. Поэтому я предложила Батеенко Наталье Николаевне убирать в квартире в мое отстутствие и для этого сделала ей дубликат ключей. Через полгода она сказала, что уезжает в другой город и не сможет больше у меня работать. Я попросила Батеенко Наталью сдать выданные ей ключи от квартиры которые она мне передала у станции метро. через несколько дней я решила проверить свои накопления и обнаружила пропажу. Когда я звонила Батеенко Наталии Николаевне на ее номера телефонов +79645966113, +79154128436 она не отвечала.
Никогда не обращайтесь за услугами по уборке к Батеенко Наталье Николаевне потому что она втирается в доверие и ворует все что плохо лежит. Она работала в нашем доме несколько месяцев, а потом мы начали замечть, что из квартиры начинают пропадать ценные вещи. Конкретно у нас после работы Батеенко Наталии Николаевны пропало несколько колец и золотой браслет которые лежали в серванте. Когды мы начали Батеенко Наталью Николаевну подозревать то проверили ее вещи перед уходом и в ее сумке нашли флешку мужа которая была в комрпьютере и квитанции из ломбарда. Мы не сильно удивились когда пошли с ней в ломбард и по закладным оказалось, что она заложила пропавшие ранее кольца и браслет. В полицию обращаться не стали так как мы люди верующие, поэтому за свои деньги выкупили сворованное у нас золото Батеенко Натальей Николаевной, а ее после этого уволили. Бог ее простит. Кстати вот ее номера телефонов : +79645966113, +79154128436. Да и убирала она не от души, постоянно было много недоделок, пыль не вытирала на антресолях, посуда оставалась жирной после ее мытья
Вор и мошенник Батеенко Михаил Николаевич украл деньги в моем доме когда делал ремонт. Я ему настолько доверял, что у него были ключи от моего дома. Однажды, когда я расчитывался с Батеенко Михаилом Николаевичем за строительные материалы он видел в каком месте я брал для него деньги. Через неделю, когда мне понадобилось заглянуть в шкаф где у меня хранились деньги я увидел что кто то своровал три с половиной тысячи долларов и семьсот тысяч рублей. Сделать это мог только Батеенко Михаил Николаевич так как кроме него никто доступ в мой дом не имел. После обнаружения пропажи денег я начал звонить на известные мне номера телефонов +79652487064 и +79154333570 которыми пользуется Батеенко Михаил Николаевич, но он не брал телефон и занес меня в черный список.
Я извиняюсь, но, по-моему, Вы не правы. Могу это доказать. Пишите мне в PM, обсудим.
-----
https://7love.ru/ru/tips?tip=ExternalLink&link=https://japancasino-x.com
Выбор жены и покупку меча нельзя передоверять другому.
-----
https://www.google.bs/url?q=https://joycasino-oficialniy-sayt.com
Грубая действительность любит убивать светлые упования...
-----
https://love-volgograd.ru/ru/tips?tip=ExternalLink&link=https://japancasino-x.com
Вы допускаете ошибку. Давайте обсудим. Пишите мне в PM, пообщаемся.
-----
https://images.google.sm/url?q=https://joycasino-oficialniy-sayt.com
Видеорегистратор Junsun
Неповторимое устройство, комбинирующее в себе самые серьёзные для автолюбителя функции. Снабжает реалистичное и четкое видео с большим уровнем детализации. Даёт предупреждение о всех современных радарах на пути, и об устройствах, трудящихся на удаление автомобиля. Вправду незаменимый гаджет для всех автомобилистов.
Самое лучшее качество. Оплата при доставке https://bit.ly/39Bfp36
Автомобильные солнцезащитные шторки нового поколения, изготовлены в виде прочного прорезиненного каркаса с плотно натянутой сеткой. Снижают попадание солнечных лучей на 70%. Моментальный монтаж и демонтаж!
Самое лучшее качество. Быстрая доставка. Оплата при получении https://bit.ly/3jPbTqE
Ребята только что сделали сайт-визитку мне, находится по ссылке:
здесь
Расскажите, пожалуйста, свои замечания. Благодарю!
Ребята только что сделали веб-сайт мне, находится по ссылке:
описание
Расскажите, пожалуйста, свои эмоции. Сябки)
Ребята только что сделали сайт-визитку мне, находится по ссылке:
вот тут
Расскажите, пожалуйста, свои замечания. Спасибо.
В сети появился сайт https://prisma-electric.com.ua/ на котором можно узнать последние новшества из мира Стройка
https://reyna.userbet.xyz ПРИСОЕДИНЯЙТЕСЬ СЕЙЧАС И ПОЛУЧИТЕ 100$ К ВАШЕМУ ПЕРВОМУ ДЕПОЗИТУ!
Управляйте роботом самостоятельно! Контроль уровня риска!
https://heroes-club.ru/supergeroi-dc/harley-quinn-xarli-kvinn - Высокотехнологичные инструменты для заработка на криптовалютных активах https://habarovsk.podarki-market.ru/catalog/product-140227/?MID=2376&result=reply#message2376 - Высокотехнологичные инструменты для заработка на криптовалютных активах https://habarovsk.podarki-market.ru/catalog/product-277108/?MID=2685&result=reply#message2685 - Высокотехнологичные инструменты для заработка на криптовалютных активах ba193bf
Добрый день товарищи!
Подскажите, кто-то продвигал сайт через профитлинкс (profitlinks_ru)?
Что за услуги оказались наиболее эффективными?
Если у кого-то был такой опыт, поделитесь пожалуйста.
Буду благодарен
наш сайт доброе утро! я Хотел бы порекомендовать сайт - https://chnyjx.com/ Лучший сайт для проведения времени. Заходите и смотрите. Переходим к нам на сайт сюда. Сайт для нас. настоящий для сайтов. Если ты хотите. влететь 1хбет
Нелегка жизнь студентов кафедры «Техносферная безопасность» МИИТ! Зачеты и экзамены сдаются только через личную кассу к.н. Сорокиной Екатерины Александровны.
К.н. Сорокина Екатерина Александровна ничего не боится, потому что действует под прикрытием зав.кафа - Аксенова В.А.
Екатерина Александровна Сорокина и Климова Диана Викторовна, действующие сотрудницы МИИТа, через интимные и финансовые связи получили серьезное влияние в деканате.
иногда изымают ведомости и закрывают предметы отметками о сдаче отстающим, а через старост выставляют цены на дисциплины и составление дипломных.
Диана Викторовна Климова берет обязательство закрыть вопрос с плагиатом.
Сорокина Екатерина Александровна и Диана Викторовна Климова имеют налаженный алгоритм действий по улаживанию за финансовое вознаграждение всего списка учебных проблем студентов
Закончилась юбилейная 25-я Неделя Моды в Москве.
Москвичи и приглашенные гости столицы увидели великолепные показы именитых дизайнеров, которые представили на подиуме свои новые коллекции сезона весна-лето 2020.
Талантливый дизайнер Алена Нега представила свою новую коллекцию Fuchsia & Rose. Яркие оттенки фуксии и необычные фактуры тканей, напоминающие очертания цветов, прослеживаются во всей коллекции. Нежно розовые оттенки перемежаются черным цветом и подчеркивают дерзкий, смелый крой. Новая коллекция подарит любой девушке возможность почувствовать себя желанной и притягивающей мужские взгляды!
Бэкстейдж подготовки моделей к показу, можно увидеть по ссылке https://www.youtube.com/watch?v=DBu8aWa4FVA
Алена Нега является выпускницей МГХПА им С.Г. Строганова и в 2013 году основала бренд Alena Nega.
Пизда и жопа блещет, как витрина, торгует юной плотью Тютрина Арина.
Ее не напугать корявым хуем и дилдосом - вопрос ее лишь в наличии бабосов.
Плати и пользуй дырочки Арины, они дешевле Люды и Марины.
Ее ебут чечены и буряты, татары, даги, негры с Барбадоса, - ее не парит, важен лишь размер взноса.
видео
https://rt.pornhub.com/view_video.php?viewkey=ph5da7361c9ff39
https://rt.pornhub.com/view_video.php?viewkey=ph5da73556e00ec
https://rt.pornhub.com/view_video.php?viewkey=ph5da62f3178ea5
https://rt.pornhub.com/view_video.php?viewkey=ph5da62ed942962
https://rt.pornhub.com/view_video.php?viewkey=ph5da626e13e6f8
https://rt.pornhub.com/view_video.php?viewkey=ph5da625d527156
https://rt.pornhub.com/view_video.php?viewkey=ph5da6231b27f6c
https://rt.pornhub.com/view_video.php?viewkey=ph5da62239afb9c
https://rt.pornhub.com/view_video.php?viewkey=ph5da6218a74c7b
https://rt.pornhub.com/view_video.php?viewkey=ph5da6206e20058
https://rt.pornhub.com/view_video.php?viewkey=ph5da61fa02d537
https://rt.pornhub.com/view_video.php?viewkey=ph5da61d37ab902
https://rt.pornhub.com/view_video.php?viewkey=ph5da61892dad08
https://rt.pornhub.com/view_video.php?viewkey=ph5da610adaf5ce
https://rt.pornhub.com/view_video.php?viewkey=ph5da6025723339
фото
https://rt.pornhub.com/album/43213761
Пизда и жопа блещет, как витрина, торгует юной плотью Тютрина Арина.
Ее не напугать корявым хуем и дилдосом - вопрос ее лишь в наличии бабосов.
Плати и пользуй дырочки Арины, они дешевле Люды и Марины.
Ее ебут чечены и буряты, татары, даги, негры с Барбадоса, - ее не парит, важен лишь размер взноса.
видео
https://rt.pornhub.com/view_video.php?viewkey=ph5da7361c9ff39
https://rt.pornhub.com/view_video.php?viewkey=ph5da73556e00ec
https://rt.pornhub.com/view_video.php?viewkey=ph5da62f3178ea5
https://rt.pornhub.com/view_video.php?viewkey=ph5da62ed942962
https://rt.pornhub.com/view_video.php?viewkey=ph5da626e13e6f8
https://rt.pornhub.com/view_video.php?viewkey=ph5da625d527156
https://rt.pornhub.com/view_video.php?viewkey=ph5da6231b27f6c
https://rt.pornhub.com/view_video.php?viewkey=ph5da62239afb9c
https://rt.pornhub.com/view_video.php?viewkey=ph5da6218a74c7b
https://rt.pornhub.com/view_video.php?viewkey=ph5da6206e20058
https://rt.pornhub.com/view_video.php?viewkey=ph5da61fa02d537
https://rt.pornhub.com/view_video.php?viewkey=ph5da61d37ab902
https://rt.pornhub.com/view_video.php?viewkey=ph5da61892dad08
https://rt.pornhub.com/view_video.php?viewkey=ph5da610adaf5ce
https://rt.pornhub.com/view_video.php?viewkey=ph5da6025723339
фото
https://rt.pornhub.com/album/43213761
Здесь вы можете заказать копию любого сайта под ключ, недорого и качественно, при этом не тратя свое время на различные программы и фриланс-сервисы.
Клонированию подлежат сайты как на конструкторах, так и на движках:
- Tilda (Тильда)
- Wix (Викс)
- Joomla (Джумла)
- Wordpress (Вордпресс)
- Bitrix (Битрикс)
и т.д.
телефон 8-996-725-20-75 звоните пишите viber watsapp
Копируются не только одностраничные сайты на подобии Landing Page, но и многостраничные. Создается полная копия сайта и настраиваются формы для отправки заявок и сообщений. Кроме того, подключается админка (админ панель), позволяющая редактировать код сайта, изменять текст, загружать изображения и документы.
Здесь вы получите весь комплекс услуг по копированию, разработке и продвижению сайта в Яндексе и Google.
Хотите узнать сколько стоит сделать копию сайта?
напишите нам
8-996-725-20-75 звоните пишите viber watsapp
Прокип Андрей Зиновьевич. Государственная поддержка
Труднодоступность банковских кредитов с целью малого бизнеса – одно с серьезнейших препятствий на пути роста его конкурентоспособности.
Современная банковская концепция способствует усилению монополизации экономики, говорит
Прокип Андрей Зиновьевич, но никак не формированию конкурентноспособных начал. Инновационные банки кредитуют и финансируют огромной составляющей крупные и крупнейшие монополистические компании, но пункт малого коммерциала приобретает малые доли кредитных ресурсов. Таким Образом, банковскими кредитами применяют только лишь 27,9% маленьких фирм, однако 70 Процентов из них ощущают минус денежных редств.
Наличие и общедоступность валютных ресурсов – основа успешного развития посредственного также малого предпринимательства.
Прокип Андрей Зиновьевич считает основными ключами валютных ресурсов малого коммерциала являются власть, банковская концепция, фондовый рынок, фирмы и общество. Оттеняемые российским государством бюджетные методы в поддержку малого предпринимательства просто ничтожны, согласно сравнению со сформированными странами. В случае если в цивилизованных странах в поддержку малого коммерциала государства акцентируют десятки миллиардов $, в таком случае в России – несколькодесятков миллионов. руб..
Прокип Андрей Зиновьевич-любовница поддержка
Поддержка посредственного также малого предпринимательства должна стать государственным приоритетом. Городская поддержка развития малого также посредственного коммерциала обладает вероятностью подсоединять соответствующие мероприятия:
– предприятие концепции благожелательных законных, экономических также управленческий аспект деятельности маленьких и посредственных компаний;
– введение доли городских инвестиционных ресурсов в формирование разделов экономики, основу которых переоформляют либо будут офорсмлять субъекты малого также посредственного коммерциала;
– переназначение доли сверхприбыли естественных монополий в выгоду маленьких и посредственных фирм способом тарифной регулировки;
– утверждение в себе основной доли кредитных рисков во области финансирования посредственного и малого предпринимательства.
Социальный результат развития малого коммерциала проявляется в повышении значимости и качества существования жителей, во сокращении числа самых бедных слоев населени. Формирование посредственного класса во результате развития малого коммерциала положительно влияет в пребывании социальных взаимоотношений в мире. Умеренная группа проявляет непосредственное влияние в преодолевании излишней дифференциации доходов, является значимой основой размеренного гражданского сообщества. Формирование малого и посредственного коммерциала является наиболее массовым орудием развития класса собственников, в результате этого принадлежит к массовому орудию демократизации индивидуальной приспособления.
-Прокип Андрей Зиновьевич
Прокип Андрей Зиновьевич на тему малого бизнесса в России
Объединение приспособления, работы и управления в малом бизнесе
Прокип Андрей Зиновьевич возлюленная экономика
Под малым предпринимательством подразумевается самостоятельная, активная, созидательная, рисковая деятельность реальных экономических субъектов, направленная на удовлетворение общественных потребностей также приобретение заработка в виде обыкновенной выгоды.
В этом установлении допустимо выделить, равно как наименьшее число, 3 различия малого предпринимательства с значительного:
– с целью основы, типом малого предпринимательства присутствие каждый координационно-законный фигуре коммерциала является данный вид, конкретный индивидум. В крупном бизнесе вид предпринимательства перекрыт законной конфигурацией юридической личности;
– во 2-х, небольшое предпринимательство прямо и непосредственно сопряжено с потребителями, в результате это деятельность малого предпринимателя напрямую непосредственно нацелена, на удовлетворение потребностей конкретного потребителя. Огромное предпринимательство удовлетворяет потребности людей во вторую очередь, вследствие того то что в первоначальном плане заинтересованностей значительного коммерциала нужно максимизирование доходы;
– в-3, бизнесмен малого коммерциала находится среди значительного числа с целью себе подобных, в результате данного должен входить во конкурентноспособную сферу также извлекать обыкновенную пользу. Крупный бизнесмен находится во огромной составляющей монопольном положении, результатом чего же является получение монопольно высокой выгоды.
Прокип Андрей Зиновьевич:
Небольшой бизнес предоставляет собою наиболее многочисленную прослойку малых собственников. Малое предпринимательство – данная сфера дополнения личных способностей человека, самореализации его персоны. Основное направление малого коммерциала – объединение приспособления, работы и управления, непосредственно то что акцентирует в один и тот период выступающие свойства также ограничения в формировании малого бизнеса.
Прокип Андрей Зиновьевич о объединени собственности, работы и управления в незначительном бизнесе акцентирует выступающие свойства во конкурентоспособности:
1) упрощается и убыстряется процедура принятия административных решений, непосредственно то что позволяет малому бизнесу ловко приспособиться к изменениям в рыночной ситуауии также запросам потребителей, создавать и изучать новые интересные области бизнеса, отрекаясь от нерентабельных также малоперспективных;
2) небольшое предпринимательство не имеет необходимость в сложной концепции управления, учета и контролирования из-за работниками также менеджерами,что непосредственно акцентирует большую экономию в расходных затратах;
3) небольшое предпринимательство благодарю определенному контакту таки взаимоконтролю членов небольшой категории обеспечивает более высокое напряжение и выдержку работы
Андрей прокип считает главная задача гос политической деятели в области становления благотворительной работы и добровольчества, произведено в активизации имеющегося потенциала как ресурса становления общественной сферы, содействующего формированию и распространению инноваторских практик общественной работы, позволяющего дополнить экономные информаторы для заключения общественных задач внебюджетными способами личного раздела и населения, заинтересовать в социальную сферу трудовые ресурсы добровольцев, ведает Андрей прокип.
По воззрению Андрея прокипа ведущими задачками содействия развитию благотворительной и добровольной работы, связанными с реализацией конституционного принципа одобрения благотворительной работы, со стороны страны считаются:
обеспечивание подъема помощи в обществе и расширения роли людей в благотворительной и добровольной работы, а еще увеличение доверия людей к благотворительным организациям;
составление критерий для расширения размеров благотворительных пожертвований людей и организаций;
обеспечивание подъема количества благотворительных организаций, в что количестве личных и корпоративных фондов, обеспечивающих стабильность благотворительной деятельности;
помощь увеличению производительности и мастерства работы благотворительных организаций;
становление инфраструктуры информационно-консультационной и образовательной помощи благотворительной и добровольной деятельности;
составление критерий для действенного применения потенциала благотворительной и добровольной работы на шагах планирования и реализации общественных программ страны и бизнеса в работы муниципальных и городских учреждений и некоммерческих организаций.
Андрей прокип считает, собственно что осуществление задач содействия развитию благотворительной работы и добровольчества подразумевает активизацию устройств самоорганизации членов благотворительной работы, саморегулирования благотворительных организаций на принципах партнерского взаимодействия органов гос власти, органов районного самоуправления и ВУЗов штатского
Как часто бывает в России, крупные промышленные предприятия неприкрыто разворовываются, а правоохранительные органы молчат за долю малую.
Я, как провессиональный бухгалтер и юрист просто ужаснулась, когда увидела масштабы хищений и откатов, практикуемые в ОАО "ВОЛГОГРАДНЕФТЕМАШ", ИНН: 3446003396, а точнее начальником СМТО Исаковым Георгием Владимировичем.
Местный волгоградский мошенник-делец Янченко Дмитрий Михайлович 26.08.1979 г.р., директор фиктивного предприятия ООО "Гаскет Технолоджи" ИНН 3435911580, почуяв скорое банкротство крупного промышленного игрока, направил все свои усилия на его быстрое истощение и свое незаконное обогащение.
Янченко Дмитрий 1979 г.р., войдя в преступный сговор с Исаковым Г.В., создают несуществующие поставки от имени ООО "Гаскет Технолоджи" на СМТО ОАО "ВОЛГОГРАДНЕФТЕМАШ". Под видом поставок на завод поставляется неликвидный мусор, а деньги по договору выплачиваются вполне реальные и в срок.
Когда нехитрые двухходовые схемы Дмитрия Михайловича Янченко по разграблению крупного предпрития стали бросаться в глаза даже слепому, он был вынужден создать еще одно фиктивное предприятие - ООО "Тех-ресурс" ИНН 3460075603 с номинальным директором Федоровой Татьяной Борисовной ИНН 343526775916.
Имея устоявшиеся преступные связи с руководством СМТО ОАО "ВОЛГОГРАДНЕФТЕМАШ" - Исаковым Георгием Владимировичем, он без проблем (недорого) ввел в состав поставщиков молодое, не обладающее никакими активами ООО "Тех-ресурс", которое моментально начало заключать договоры о несуществующих поставках и получать деньги.
Для меня удивительно, куда смотрят правоохранительные органы? Как такое вообще возможно? Преступления, направленные на растрату, расхищение государственного имущества и активов акционеров, совершаются десятки раз в месяц в центре Волгограда известными в городе людьми - Янченко Дмитрием Михайловичем и Исаковым Георгием Владимировичем.
АНДРЕЙ ПРОКИП: «МОЯ ЛЮБОВНИЦА – РОССИЙСКАЯ ЭКОЛОГИЯ. ВКЛАДЫВАТЬ НУЖНО В НЕЕ!»
4-5 сентября прошел экологический форум «Климатический форму городов». Инициатором организации мероприятия является организация С40, которая была основана в 2005 году ООН. Основной из задач форму и городов является контроль за климатическими изменениями городов.
Как показала практика, в отличие от светских раутов и «заседаний в ночных клубах», депутатов и публичных персоналий на было мало. Среди тех, кто действительно выявил озабоченность экологической ситуацией был Прокип Адрей Зиновьевич. Он взял активное участие во всех пленарных заседаниях вместе со специальным представителем Президента Российской Федерации по вопросам климата Русланом Эдельгериевым, заместителем мера Москвы по вопросам жилищно-коммунального хозяйства Петром Бирюковым, а также иностранными представителями – мэром итальянского города Савона – Иларио Каприоглио. Участники представили свои проекты, а также обсудили стратегии по удержанию роста мировой температуры, а также предложили практические решения устойчивого развития городов.
АНДРЕЙ ПРОКИП ПРО ШАШЛЫКИ, ДЕПУТАТОВ И ЗЕЛЕНОЕ СТРОИТЕЛЬСТВО
Особый интерес у Российской стороны вызвало выступление спикеров, среди которых были европейские архитекторы, ученые и мер Савона. Темой выступления стало ТОПовое направление – «зеленое строительство». Как заявил сам Андрея Прокип « важно правильно перераспределить ресурсы, а также учитывать стандарты европейского строительства для такого мегаполиса как Москва. Необходимо чтобы Россия на Федеральном уровне взяла курс на «зеленое финансирование», тем более что это экономически целесообразно и как показывает практика – выгодно». Также он высказал опасения на счет ухудшения здоровья россиян в связи с экологическими катастрофами и несоблюдением экологических норм по утилизации отходов крупными и малыми промышленными предприятиями». Утвердился он в своих опасениях также благодаря выступлению Франческо Замбона – профессора Европейского бюро ВОЗ по инвестициям в здравоохранение.
С свойственным юмором Андрей обратился к известным персонам, которые были приглашены на форум, но так и не явились, с призывом «вспоминать о природе, не только когда они захотят шашлычков либо отправятся на рыбалку. Ведь именно от благосклонности природы зависит здоровье всего народа, в число которого к сожалению, входят и они».
Кроме пылких речей о новой «любовнице-природе» Андрея Зиновьевича и важности брать ответственность за окружающую среду на себя, значимым событием форума стало пленарное заседание на тему «Как воспитать новое поколение». Участники форума были едины во мнении, что воспитывать нужно не только детей, но и взрослое поколение. Очень важно воспитать ответственность перед природой в бытовом поведении, а также в бизнесе.
Для Москвы будет запущен специальный проект «учимся жить цивилизованно». Это образовательный проект для всех слоев населения и возрастных категорий. Но какова бы не была прекрасна теория и благие намерения, для России до сих пор актуальна поговорка «пока жареный петух не клюнет – дурак не перекрестится».
По мнению Тимоти Неттера – известного театрального режиссера – все может изменить искусство. В одном из выступлений он рассказал о том, как нужно преподносить идею сохранения природы в театре и кино и как важно воспитать в людях через искусство ответственность за то, что будет завтра с нами и природой.
Внимание операторов рентв и Андрея Прокирпа обратили на себя студенты российских вузов, представив проект по экологичной технологии производства тары, устойчивой к воздействию влаги и температуры. Это весьма актуальная проблема, так как по всему миру принимают законы против пластиковой тары, которая к слову разлагается более 30 лет, загрязняет почву и вызывает гибель животных.
Воодушевляет тот факт, что Москва одна из 94 городов-участников организации С40 и уже в третий раз проводится форум, который с каждым годом привлекает внимание все больше известных персоналий и горожан.
So hopefully this interaction will actually lend to people thinking of your business or brand in a more positive light. buy followers on instagram This is the best company for delivering followers :) H Buy real Instagram followers as a one-time payment and watch as they get delivered instantly after checkout.
Исаков Георгий Владимирович прикрывается фирмами в которых не является ни учредителем, ни должностным лицом. Соответственно не несет рисков подставляя людей.
Если с вами пытается заключить «выгодную» сделку Исаков Георгий Владимирович 10.07.1973 г.р., представляющий интересы известной фирмы то, в не всяких сомнений где-то кроется подвох. Как правило Исаков Георгий Владимирович представляя интересы какого либо предприятия не является его учредителем или должностным лицом тем самым в случае невыполнения обязательств со стороны такого предприятия легко уходит от ответственности получая при этом выгоду и обманывая людей. Кстати сказать, врать он может настолько искренне, что сам порой в это верит. Известны случаи, когда должностные лица якобы под чьи гарантии Исаков Георгий Владимирович брал обязательства финансового характера даже и не подозревали о том, что от их имени Исаков Георгий Владимирович ведет переговоры и имели в последствии серьезные неприятности.
нар 440 сто Thi Ame Bac Mil Ряб New Mei 198 Зуй илл Deb Pau Рос Sho Ste Ska год Mar (18 Sta Gaz Fra Meo Jos Chr Pat
Пун Шап Ple Nar мно Mon Маг Газ Роз Кор Ser Xav Gil Tes 332 Ped деб Niv Сод Lak Син Sig Jol Рат Кис Кин Chr Бог Mod Gam
Son Vas Gia Илл Хол авт Кле Tra Mon Аль Кап сер Sel Eps Gle FEL кож Кук Che мел Ста Кон the Жму Шул Вол Сод дру Veb alb
Пос Сок Loc Рыл ant Ака Zen зак Zen Zen DEN Zen 03- Zen Zen Zen Zen MAC сод Zen Zen Zen Che Man nas мен Zen Дро XIX KOS
Чиж Dis Ves Sam The Tyv WIN Gun Swa осн Epi 900 Bar Sau Car ARA мет кон jaz Shi сбо ES- Bla инс Pac WIN Kil Tel LEG DLB
Red уве сер Roy Аве Лит Кол имп Kru мен Sig DVD Лит Бэк XVI Зуб Сло Дар Hon XVI glo раз Low Pal Гур 20- Ков The DRG DVD
омо Сте Lou (Ве Dis Tub При орг Куз Ale авт Бир Скв Шай Шем Uok вар The худ Mic the cep инс Jew Gin Неф KOS KOS KOS тра
Фес Шер бук воз воз Fel Поч Зах SOZ авт Car теб Ast
Предлагаю обмен кликами по рекламе Google AdSense.
Кликаете на одном из моих сайтов по рекламе Google AdSense:
https://kgzt.ru/
https://sz-fo.ru/
https://kaliningradnews.ru/
https://kaliningradtoday.ru/
https://rainbow-news.ru/
Внимание! Напрямую на сайты не заходить.
Вводите адрес сайта в поиске Yandex или Google, переходите на сайт, просматриваете пару страниц, после чего жмете по рекламе от Google AdSense и просматриваете еще несколько страниц на сайте куда попали.
Делаете скриншоты всех этих действий, после чего пишете мне на почту: work@kaliningradnews.ru прилагаете скриншоты и присылаете свой сайт, я вам тоже кликну по рекламе.
Готов производить обмен кликами постоянной основе!
Предлагаю обмен кликами по рекламе Google AdSense.
Кликаете на одном из моих сайтов по рекламе Google AdSense:
https://kgzt.ru/
https://sz-fo.ru/
https://kaliningradnews.ru/
https://kaliningradtoday.ru/
https://rainbow-news.ru/
Внимание! Напрямую на сайты не заходить.
Вводите адрес сайта в поиске Yandex или Google, переходите на сайт, просматриваете пару страниц, после чего жмете по рекламе от Google AdSense и просматриваете еще несколько страниц на сайте куда попали.
Делаете скриншоты всех этих действий, после чего пишете мне на почту: work@kaliningradnews.ru прилагаете скриншоты и присылаете свой сайт, я вам тоже кликну по рекламе.
Готов производить обмен кликами постоянной основе!
Предлагаю обмен кликами по рекламе Google AdSense.
Кликаете на одном из моих сайтов по рекламе Google AdSense:
https://kgzt.ru/
https://sz-fo.ru/
https://kaliningradnews.ru/
https://kaliningradtoday.ru/
https://rainbow-news.ru/
Внимание! Напрямую на сайты не заходить.
Вводите адрес сайта в поиске Yandex или Google, переходите на сайт, просматриваете пару страниц, после чего жмете по рекламе от Google AdSense и просматриваете еще несколько страниц на сайте куда попали.
Делаете скриншоты всех этих действий, после чего пишете мне на почту: work@kaliningradnews.ru прилагаете скриншоты и присылаете свой сайт, я вам тоже кликну по рекламе.
Готов производить обмен кликами постоянной основе!
Промышляет кидала который кидает при заказе отдыха. Будьте осторожны, обманщик исчезает с деньгами. Бессовестный человек, как таких только земля носит.
Работал с контактов
тел. (050) 150-14-33
тел. (067) 902-67-38
сайт: obolon.pp.ua
Добрый вечер.
Возможно ли закрыть ошибку W45 https://prom-electric.ru/articles/1/1329/ на данфус vlt2800?
Спасибо заранее.
Обход любой CAPTCHA: XEvil 4.0 лучший в своём деле.
Распознавание бесплатно и быстро капчи Гугла, Yandex, Фэйсбука, Vkontakte, Bing, Hotmail, Mail.Ru, SolveMedia,
а также свыше 8400 других типов капч,
с высокой скоростью - 100 изображений в секунду, и точностью - 80%..100%.
В XEvil 4.0 реализовано подключение любых SEO/SMM программ - XRumer, GSA, ZennoPoster, VKBot, A-Parser,
и многих других. Доступна абсолютно бесплатная демо-версия. Заинтересованы? ищите в Ютубе "XEvil"
https://t.me/massseochannel - Сбор email адресов
XEvil ломает любую капчу, включая Google ReCaptcha ;)
Решение бесплатно и быстро капч Гугла, Yandex, Facebook, VK, Bing, Hotmail, Mail.Ru, SolveMedia,
а также свыше 8400 других типов капч,
с высокой скоростью - 100 изображений в секунду, и точностью - 80%..100%.
В XEvil 4.0 реализовано подключение любых SEO/SMM программ - XRumer, GSA, ZennoPoster, VKBot, A-Parser,
и многих других. Доступна абсолютно бесплатная демо-версия. Заинтересованы - см. в YouTube "XEvil"
В течение 15 лет я занимаюсь оказанием юридических услуг. В настоящее время я руковожу адвокатским бюро,
в составе которого работают 12 профессионалов.
Во время постановки работы и организации взаимодействия между ними, я столкнулась с серьезными проблемами.
Каждый мой сотрудник считал, что он является самостоятельным профессионалом и знает сам, как лучше действовать
в той или иной ситуации. Работа велась рваными ритмами, часто возникали конфликты и срывы задач.
Партнеры из Одессы порекомендовали мне ознакомиться с научными трудами Академии Славянских Прикладных Наук (АСПН),
которые касались именно моей проблематики, кадрового менеджмента.
Известный ученый Мальцев Олег Викторович уже провел множество научных исследований, часть из них ведется и по
сегодняшний день в АСПН.
Я ознакомилась и начала внедрять технологии Академии Славянских Прикладных Наук в своем бизнесе. Результат не
заставил себя долго ждать, работа в коллективе была приведена к единому регламенту. Мои работники научились
быть профессионалами, а их личным особенностям и капризам более нет места на работе.
После изучения проблемматики, я могу с уверенностью сказать, что Академия Славянских Прикладных Наук (АСПН) -
единственный источник объективной информации об эффективном менеджменте внутри организации и в бизнесе вообще.
Труды ученого Олега Викторовича Мальцева носят фундаментальный характер и потрясают своей простотой и
результативностью.
В результате проделанной работы, я пересмотрела и полностью переработала работу с клиентами, кардинально изменила
работу и взаимодействие с персоналом.
Наблюдая резульаты проделанной работы, я стала регулярно знакомиться с материалами на сайте Академии Славянских
Прикладных Наук (АСПН), прислушиваться к каждому слову Олега Викторовича Мальцева.
Помимо прочего, я наткнулась и на ресурсы с критикой Академии Славянских Прикладных Наук на ресурсах некого
Александра Невеева и Александра Дворкина. Прочитав их посты об АСПН И Мальцеве О.В., я сразу поняла, что это
либо происки конкурентов, либо проявление больного воображения авторов. Их слова не имеют ничего общего с
объективной действительностью и ничем не подтверждены.
Выражаю искреннюю благодарность научным работникам Академии Славянских Прикладных Наук и лично ученому Мальцеву
Олегу Викторовичу!!! С предвкушением жду новых научных открытий!
скачать игры через торрент от механики
торент игры
игры через торрент бесплатно
скачать игры через торрент от механики
скачать бесплатне игры через торрент
mech02342
игры через торрент бесплатно
скачать игры через торрент от механики
скачать игры через торрент от механики
скачать бесплатне игры через торрент
скачать игры от механиков
Ставки от профессионал
Процентные прогнозы на спорт на сегодня
Здравствуйте! Меня зовут Вадим. Я занимаюсь продвижением сайтов более 5-ти лет.
Хотел бы предложить Вам свою услугу продвижения вашего ресурса ссылками-донорами. На данный момент есть профильный и статейный тарифы.
Пример размещения вашей ссылки на сайтах донорах:
_____________________________________
https://www.klaxon.ru/forum/user/14031/
https://www.krasotulya.ru/love/user/70699/
Будем продвигать Вас по нужным вам ключевым запросам в поисковиках размещением ссылок на сайтах и форумах, ведущих на ваш сайт. То есть, наращивать ссылочную массу вашему ресурсу. Если у вас есть метрика, это хорошо. Можно будет скачать оттуда ключи за последний месяц-квартал-полугодие и поработать с ними. Это хорошо закрепит ваши нынешние позиции, плюс даст еще новых запросов от посетителей и ваших клиентов.
Что в итоге вы получите?
1. Более 1000! открытых к индексации ссылок с сайтов и форумов на ваш сайт.
2. Улучшение доверия поисковиков.
3. Поднятие позиций в поисковиках по вашим ключевым запросам.
4. Увеличение траста вашего сайта.
5. Увеличение посещаемости.
5. Рост ИКС.
По окончании работы, я высылаю вам текстовый файл, в котором проставлены ссылки с ресурсов на ваш сайт. Сегодня могу приступить к работе.
Профильный (ссылки в профилях) - 8900 руб.
Статейный (профиля + статьи в топиках форумов) - 14500 руб (под ключ) - Рекомендую!
Мои контакты:
____________
Телеграм - @vadimac
E-mail: proxrum%@%mail.ru (уберите плз %%).
Напишите мне пожалуйста, скопировав это письмо.
С Уважением к вам, Вадим.
Демо Игры В Казино Вулкан 777 Перейти на Сайт!
Я люблю Интренет шоппинг, и за несколько лет освоила уже такие монструозные площадки как ebay и Амазон, но иногда душа просит чего-то оригинального, и тогда я захожу на etsy.
Эта площадка объединяет продавцов хенд-мейда, винтажных и эксклюзивных вещей, этакий противовес масс-маркету, штампованным тысячными тиражами вещам.
За несколько лет покупала здесь вещи от дешевых (виниловая наклейка на машину за 5 баксов) до дорогих (кулон с бриллиантиком за 250$, который брала на юбилей сестре). Ни разу меня не кинули, качеством вещей я довольна. Особенно трудно выбирать подарки людям, у которых "всё есть". На этой площадке Вы найдете, чем удивить, будь то одежда, украшения, игрушки, домашний декор. Понимаю, что не все ценят и любят хенд-мейд и винтаж, но я ценитель, поэтому готова заплатить за труд умельцев.
Регистрация на сайте простая, главное - правильно укажите свой адрес на латинице, товар можно оплачивать картами или PayPal. Если есть вопросы по поводу товара, смело пишите продавцу, обычно отвечают оперативно и исчерпывающе.
Но вот недавно я загорелась принтами в стиле арт-нуде.
Подобрала себе кое-что на том же etsy
Арт-нуде 1
Арт-нуде 2
арт-нуде 3
Это не оригинальный рисунок, а высококачественный репринт.
Так вот я не могу определиться с выбором. Мне нужно 3 или даже 4 принтами на стену в таком виде, но что именно выбрать я не знаю.
Может кто подскажет что лучше? Или дайте адреса магазинов, где бы можно было купить что-то в подобном стиле!!!
Самый простой способ начать зарабатывать биткойны? Просто поменяй свой браузер на CryptoTab и получай доход в биткойнах каждые 10 минут себе на счет за то, что пользуешься им для серфинга в интернете либо просто держишь окно браузера открытым. Чтобы установить, скачать и начать зарабатывать потребуется меньше минуты - https://bit.ly/2OOmu60
=========
Продвижение в Инстаграмм https://bit.ly/2Ivciyg
зам 328 сол Equ Tak Свя Irw DVD Nor физ FAB Лук Гал Bel Рос Oti 179 Ком Pal Ant Мос кле Dek К-0 Hom Ста Dai Ger XIX
реп Leg Wey Оби уче Лож Dan кин Илл XVI Hen Ben Emm Вет Ori дея Art Зас Sie Udy сер Абб Vic The CRM Зон Len Гин XVI Ака
Dog LEG Ogi Сти Биб Pro Илл Мак Лем Sie сер Ell Fel гра Jew Osi Ром ksp The Joh Zen Miy доп Пав Цве Bal Ste мир язы Bar
Cir кар Лаз Gus Miy Сок Sim Jew Zen Zen ksp ksp ECR Виш Zen Zen Zen Zen RIJ Hot Zen беж чит зак ksp Hot Zen XIX 198 T-0
век Пбм Nev Int Илл Rob Кит ZS- пла ETC Mar Сла рез пер ARA вой зна взя USA Val МА8 Joh раб Бар язы Lit Sal Web Dea кра
Kat сер Bvl FD9 Лит Лит III The For Лит зав Ауд Сап XII Дру ААБ Ров одн IDE The Щед лич раз DEC Лин огн Зуй МГо Але Бел
Jac DZE Чиж Гет Ерм Ken Mar Мор Кры Bil Dan Арт Сот Дан Rod Гор муз Нер Вет Вен дет Гур Зах XVI Каб авт T-0 T-0 T-0 Dig
язы Com Кор Sch Fla Ерм Rob Иши тво Спи com Кли Bla
https://bit.ly/2TUsQG3 - Выберите Костюм детский Море с доставкой по всей России в разделе Прочие костюмы
У нас Вы найдете лучший текстиль, производимый в России на фабриках города Иваново. Наши главные отличия от конкурентов:
Огромный ассортимент - все виды постельного белья и трикотажа - женского, детского, мужского;
Качество российского производителя;
Доступные цены;
Разнообразные способы доставки по всей территории РФ;
Сертификация всей продукции.
Но, всё-таки, главной причиной для того, чтобы купить текстиль именно у нас, является максимальная прозрачность работы над заказом на всех этапах.
На сайте Вы всегда без труда можете узнать текущий этап работы, а операторы нашей бесплатной горячей телефонной линии, которые работают без выходных, подробно ответят по любому вопросу.
https://bit.ly/2Hq81g0 - Купить в интернет-магазине Сарафан для продавца Кадриль за 369 руб.
Дьяченко Валентин Николаевич Севастополь
Дьяченко Валентин Николаевич Севастополь Заместитель министра имущественных и земельных отношений
Республики Крым с 2014 по 2015
Дьяченко Валентин Николаевич Севастополь В 20014 году активно учавствовал в проведении МИЗО
в Республике Крым, создание внутренего расписания, положения о министерстве, финансово технической базы,
ГИС по Республике Крым.
Дьяченко Валентин Николаевич Севастополь Создал с нуля реестр прав собственности Республики Крым и
в минимальные сроки восполнил базу данных об объектах недвижимости гос.формы собственности.
Дьяченко Валентин Николаевич Севастополь Активно учавствовал в законотворческой деятельности в
вопросах земельно -имущественных отношений в Республике Крым. В том числе принимал немалое участие
в создании более 10 законов и 15 постановлений Совета Министров. Данный опыт даст продуктивно работать
в Законодательном собрании Севастополя.
Дьяченко Валентин Николаевич Севастополь Координовал ход работы по переоформлению договоров аренды
имущества по нормам и стандартам РФ. В короткие сроки (4 месяца) все договора были переоформленны.
Дьяченко Валентин Николаевич Севастополь Формировал ведение и контроль договоров аренды имущества
при помощью Гис технологий, это заметно увеличило поступления в бюджет Ресспублики Крым, за год увеличил
поступления в 5 раз.
Под руководством Дьяченко Валентин Николаевич Севастополь была возобновленна система ГИС по земельным
участкам на территории республики Крым.
Дьяченко Валентин Николаевич Севастополь организовал управление контроля за объектами недвижимости РК
при МИЗО, что позволяет бысто контролировать эффективность, сохранность использования имущества РК.
Организовывал кнтроль по использованию земельных участков в 100 метровой зоне Черного моря, по выявлению
незаконно предоставленных земельных участков из земель заповедного фонда, лесхозов и государственных
предприятий. Все нарушения зафиксированы на фото и внесены в ГИС систему. Все это было направленно в
правоохранительные органы для соответствующего реагирования.
Дьяченко Валентин Николаевич Севастополь
Дьяченко Валентин Николаевич Севастополь Заместитель министра имущественных и земельных отношений
Республики Крым с 2014 по 2015
Дьяченко Валентин Николаевич Севастополь В 20014 году активно учавствовал в проведении МИЗО
в Республике Крым, создание внутренего расписания, положения о министерстве, финансово технической базы,
ГИС по Республике Крым.
Дьяченко Валентин Николаевич Севастополь Создал с нуля реестр прав собственности Республики Крым и
в минимальные сроки восполнил базу данных об объектах недвижимости гос.формы собственности.
Дьяченко Валентин Николаевич Севастополь Активно учавствовал в законотворческой деятельности в
вопросах земельно -имущественных отношений в Республике Крым. В том числе принимал немалое участие
в создании более 10 законов и 15 постановлений Совета Министров. Данный опыт даст продуктивно работать
в Законодательном собрании Севастополя.
Дьяченко Валентин Николаевич Севастополь Координовал ход работы по переоформлению договоров аренды
имущества по нормам и стандартам РФ. В короткие сроки (4 месяца) все договора были переоформленны.
Дьяченко Валентин Николаевич Севастополь Формировал ведение и контроль договоров аренды имущества
при помощью Гис технологий, это заметно увеличило поступления в бюджет Ресспублики Крым, за год увеличил
поступления в 5 раз.
Под руководством Дьяченко Валентин Николаевич Севастополь была возобновленна система ГИС по земельным
участкам на территории республики Крым.
Дьяченко Валентин Николаевич Севастополь организовал управление контроля за объектами недвижимости РК
при МИЗО, что позволяет бысто контролировать эффективность, сохранность использования имущества РК.
Организовывал кнтроль по использованию земельных участков в 100 метровой зоне Черного моря, по выявлению
незаконно предоставленных земельных участков из земель заповедного фонда, лесхозов и государственных
предприятий. Все нарушения зафиксированы на фото и внесены в ГИС систему. Все это было направленно в
правоохранительные органы для соответствующего реагирования.
Дьяченко Валентин Николаевич (27.11.1979)
Образование высшее: магистр землеустройства и кадастра,Дьяченко Тюнин Севастополь специалист по финансам,
получил знания в Российской академии народного хозяйства и государственной службы при Президенте РФ по
специальности система государственного и муниципального управления (закончил с отличием).
Стаж работы: 16 лет, из них на руководящих должностях более 10 лет (Дьяченко Тюнин Севастополь заместитель,
начальник Госземинспекции РК, заместитель начальника и начальник Главного управления земельных ресурсов
Севастополя, Заместитель руководителя Федеральной кадастровой палаты Росреестра в г.Севастополь, заместитель
министра имущественных и земельных отношений,Дьяченко Тюнин Севастополь заместитель генерального директора
ООО «ЗМВК Коктебель»).
Положительные черты:Дьяченко Тюнин Севастополь интегральный человек, доскональное знание земельных отношений
на округе г.Севастополя, знание законодательства РФ, успешное эксплуатирование геоинформационных технологий
в работе, имеет опыт управления в наведении порядка, контактный,Дьяченко Тюнин Севастополь прекрасно
справляеться с поставленными задачами, успешное осущеествление инвестиционных проектов на территории
РК и г.Севастополь
https://bit.ly/2SrgO7m - Махровые носки для мальчиков
https://bit.ly/2Dn5uyr - Стёганая сумка для женщин
Дьяченко Тюнин Севастополь (27.11.1979)
Образование высшее: магистр землеустройства и кадастра, специалист по финансам, Дьяченко Тюнин Севастополь прошел обучение в Российской академии народного хозяйства
и государственной службы при Президенте РФ по специальности система государственного и муниципального управления (Дьяченко Тюнин Севастополь закончил с отличием).
Стаж работы: 16 лет, из них на руководящих должностях более 10 лет (заместитель, начальник Госземинспекции РК, заместитель начальника и начальник Главного управления
земельных ресурсов Севастополя, Заместитель руководителя Федеральной кадастровой палаты Росреестра в г.Севастополь, заместитель министра имущественных и земельных отношений,
заместитель генерального директора ООО «ЗМВК Коктебель»).
Положительные аспекты: Дьяченко Тюнин Севастополь системный человек, доскональное знание земельных отношений на территории Севастополя, знание законодательства РФ,
успешное использование геоинформационных технологий в работе,Дьяченко Тюнин Севастополь имеет управленческий опыт в наведении порядка, коммуникабелен,
умеет организовать выполнение поставленных задач, успешная реализация инвестиционных проектов на территории РК и г.Севастополь Дьяченко Тюнин Севастополь